Electrostatic Effects
The overview below briefly describes most of the behavior of static electricity. It is followed by a more detailed explanation.
Overview
Static effects (high voltage, surfaces sticking together, etc.) occur when an excess of either + or – charge becomes confined in a small volume, isolated from charges of the opposite polarity. Because of mutual repulsion, the charges try to escape confinement. As a result, the charges may move or redistribute themselves, sometimes rapidly, such as with a spark. This redistribution usually causes problems. In general, only electrons (-) actually move when + or – charges redistribute themselves. However, we can simplify the explanation by treating + charges as though they move as easily as electrons do (but usually in the opposite direction that electrons move). In order for charge confinement to occur, two steps are usually required. Two surfaces or objects may be initially neutral, but then some charge jumps from one to the other while they are very close to each other. Therefore one is – while the other is equally +. As long as they remain close, this surface charging has a negligible effect on the local environment. The second step requires that the two surfaces be pulled apart or isolated from each other. The surfaces attract each other so this step requires a small amount of pull force. Therefore some mechanical energy is required to separate them, and a larger separation requires more energy. Once the surfaces are separated, this energy becomes available for rapid movements of the charges, which can cause undesirable effects such as sparks, the clinging of dust to surfaces, and unwanted adhesion or repulsion.
Triboelectricity is the most common method of surface charging. When dissimilar materials are pressed or rubbed together, the surface of one usually becomes somewhat + while the other becomes somewhat -. At least one of the materials must be an insulator; there will be no charge exchange if both materials are metal (or at least if they are conductors on the time scale over which the contact occurs– see below for explanation). The degree of charging depends on the amount of rubbing and on how dissimilar the two are. (See triboelectric series for a listing of how much charging there is between various materials). Once charged, the two surfaces attract each other, so that at least a small amount of work will be required to pull them apart. The amount of work is usually negligible, but that work is what actually causes a voltage difference between the two surfaces once they are separated; while the surfaces were in close contact, there was zero voltage difference and the outside world had no way of detecting that the surfaces were charged (other than the fact that they stick together). Once separated, static problems can occur because the amount of charge on each of the now-separated surfaces can be significant, and each surface confines its charge to a relatively small volume. In addition, if either of the charged surfaces is part of a larger structure, the excess charge on that surface may gradually spread out, with some of it migrating to the larger structure. An example of this is the “shoes on carpet” effect, in which the negative charge (acquired by rubber soles on nylon carpet) will migrate up to the person, because the rubber is not a perfect insulator. After more walking, the soles acquire more charge, which again mostly migrates to the person.
“High voltage” results from a large excess of either + or – charge being confined on a relatively small object (a small volume). If a charged object or surface contains a given amount of charge, its voltage becomes higher when it is taken to a location far from earth ground and far from a significant amount of charge of the opposite polarity. The amount of “damage” that can be done (the electric energy stored) by the charged object is proportional to the object’s voltage multiplied by the amount of charge it contains, and the voltage is approximately proportional to its charge divided by the lesser of either its diameter or the distance to the nearest earth ground. This energy can be released if the excess charge (which is all either + or -) rapidly leaves the confining volume, driven by mutual repulsion. Charges may escape by jumping directly into the air (sparking), by jumping onto a passing dust particle (the dust often helps create a spark so that a bit of charge can escape, but the spark makes the dust acquire an opposite charge, so it remains stuck to the surface of the charged volume), or by flowing to earth ground if the charged volume touches either ground or touches a wire connected to ground. There are formulas that show how to estimate voltage and other parameters. If an object was initially strongly charged + while far from both earth ground and from any significant amount of – charge, the object will be at high positive voltage, which means that sparks can jump a long distance from it. (Sparks can jump at least 1 cm per 10 kilovolts). Counterintuitively, if the + charged object is then brought close to earth ground or close to – charges, its voltage will decrease significantly even though its charge remains the same.
As an example of this voltage decrease when brought close to ground, imagine a 100 cm diameter isolated metal sphere that is hanging from a high ceiling, far from any object or the ground, and it has been given an amount of + charge that corresponds to +100 kV (100,000 volts) which is measured with respect to earth ground. (Earth ground is usually defined as zero volts.) If a long wire is connected at one end to ground and the other end is brought to within 10 cm from the sphere, most of the + charge will suddenly spark over to the wire and will flow down to the earth. The wire is now pulled away, and the sphere is then charged back up to +100 kV. It is now in the same state as before the spark. Then the sphere is lowered (without letting any charge escape) to within 1 cm of the floor, which is at earth ground. Now the sphere’s voltage will have decreased to below 10kV volts, even though none of the + charge had escaped. If a grounded wire is then held near one side of the sphere, the wire’s tip would have to be about 1 cm away (instead of 10 cm) to get a spark. (The sharpness of the wire’s tip helps initiate sparking, which is why the charge will spark to the wire instead of to the flat floor below it, which is also 1 cm away.) The amount of electric energy and potential damage of this spark is about 1/10 that of the first spark. The reduction in voltage (and energy) happens because some – charge from the earth is attracted up to the floor just under the (positive) sphere. The floor has a large area, so the amount of – charge on the floor is almost as much as the amount of + charge in the sphere. Therefore the total of +charge on the sphere added to the – charge nearby on the floor brings the excess + charge in the vicinity of the sphere down to about 1/10 of what is on the sphere alone. By bringing the ground closer, we have introduced a significant amount of – charge near the sphere. Therefore the mutual repulsion of all the + charge on the sphere is reduced, so the electric energy available is also reduced.
With a perfect insulator, any + or – charge that is trapped inside will simply remain where it is. A charge deposited on a perfect insulator’s surface cannot move along that surface, but the charge may be deliberately removed from the surface (or replaced by a different charge) by actions from outside. A conductor (metal) is the opposite of an insulator. Metals allow charge to move freely and rapidly both inside and on the surface. If a + charged object is brought near the left side of a metal sphere, electrons inside the metal will feel the pull of the + charge, and they will travel to the left as far as they can go, which is the left surface of the sphere. This movement takes only a few nanoseconds and when these electrons build up on the left side of the sphere, their presence on the left side repels the other electrons inside the sphere. The repulsion has just enough force to counteract the attractive force of the + charge that is just left of the sphere. This new distribution of electrons on the surface of the metal sphere therefore stops all motion of electrons inside of the sphere (an equilibrium). The sphere now has excess electrons on the left surface (only within a layer that is one atomic diameter thick). Because many electrons were attracted to the left, there is a shortage of electrons on the right surface. This shortage is the “+” charge. We can interpret that the + charged object attracted some – charge toward the left surface of the sphere and simultaneously repelled some + charge toward the right surface of the sphere. In this state, if a grounded wire is touched to the right side of the sphere, the + charges on the right side will flow down the wire to the earth, because they continue to be repelled from the + object that is left of the sphere. Then the sphere will have an overall – charge, because it just lost some of its + charge. This method of charging is called “charge induction” and it is the other common source of unintended static charge (besides triboelectricity). The distribution of charges on a metal surface is further discussed below (see Fig. 3 below) along with charge induction (Fig.4).
There is a continuum between “perfect insulator” and “perfect conductor”. Samples are often characterized within this continuum by their resistance. A very high resistance means an almost perfect insulator, while very low resistance means an almost perfect conductor. However, in order to understand typical electrostatic problems more clearly, it is better to characterize samples by their “conductive time constant”, instead of resistance. As mentioned above, the charges in metal rapidly move around to compensate when a charged object is brought near the metal. Once the redistribution is complete, it is exactly balanced so that all of the electrons inside the metal will simply remain wherever they are, as opposed to being attracted to or repelled from the nearby charged object. In solid copper or aluminum with typical dimensions of centimeters, this redistribution requires only a few nanoseconds, but in a hollow shell of the same metal, 10-100 times that long may be required. Paper and cardboard are slightly conductive, and are better conductors if the humidity is high. At 40% relative humidity, a cubic foot cardboard box (30 x 30 x 30cm) will shield its inside from the effect of exterior charges in a way similar to the way a hollow metal shell would, except that the cardboard at 40% RH may require 1 – 10 seconds to do it. If an external charge is brought near a cardboard box and is then held in place for over 10 sec, the box will have enough time to shield its inside from the effect of the external charge. Therefore, in the timescale of 10 sec or longer, the cardboard box acts as a conductor. If an external charge is instead brought close to the box but the charge is then moved around rapidly, the small number of mobile charges in the cardboard will not have enough time to redistribute properly, and the box will act as an insulator. Glass, natural fabrics, concrete, and water-based paints also have the property of being “fast insulators and slow conductors”. This means for example that glass can be charged both by induction and conduction, but only if it is done slowly. Only conductors can be charged by induction and/or conduction.
Air normally contains both + and – air ions, and the air itself is actually a conductor over a time scale of hours. When ionizers are used to increase the number of + and – ions significantly, the ion-enriched air will generally have a conductive time constant of a second or less, and is thus capable of discharging any charged object rapidly. There are formulas for the number of ions, discharge time, and resistivity of air.
A more detailed explanation of electrostatic effects
For charging: Most matter is electrically neutral. Under certain circumstances however, an outer electron may be able to leave the atom it is orbiting. When an electron leaves, the atom that remains behind will have an excess positive charge, and the electron’s destination will have an excess negative charge. This effect happens frequently at the interface between two dissimilar materials, such as rubber and nylon, even if the two materials are in contact only briefly. Generally, one of the materials (rubber likes to steal electrons) will attract electrons from the surface of the other material (nylon likes to give away electrons). This is the famous “shoes on carpet” effect, and it causes static charging. If a sheet of rubber and a sheet of nylon were initially in contact but then separated from each other, nylon will have an excess of positive charge because it had lost electrons during the contact, and rubber will have an excess of negative charge. Then they will continue to attract each other even though they are separated. The most stable state for this system is for the two sheets to be in close contact, as they are before being pulled apart. When the sheets are separated, the electrons on the rubber will try to go back to the nylon by various routes, such as by sparking or by ionizing the air, by charging dust grains and hitching a ride on them, or by reuniting the two sheets via the attractive force. These attempts at reuniting cause most of the undesirable static effects.
As an example of friction charging, consider a sheet of nylon and one of rubber, each having an area of one square meter. If the sheets are pressed together face to face, only a surprisingly small fraction of their surfaces will be in contact. If they are forced together with significant pressure or especially if they are rubbed together, much more of the rubber and nylon surfaces will eventually come into mutual contact, at least for a moment. When in contact, something like a chemical reaction occurs, similar to the reaction between the two electrodes of a battery (See triboelectric series, which lists the amount of charge transferred between dissimilar materials). The rubber surface attracts a tiny fraction of the electrons on the nylon surface. See frame 1 of Fig. 1.
The unit of “charge” needs to be defined in order to understand electrostatic parameters. An “amp second” is the most commonly used measure of charge, and is also known as a Coulomb (C). It is literally the amount of charge that flows through a wire if one amp DC flows for one second, and is equal to 6.25×1018electrons. In the nylon/rubber example, the two sheets are rubbed together until 10-5 amp sec of electrons transfer from the nylon surface to the rubber surface (both surfaces are 1 m2). This is 6.25×1013 electrons (= 6.25×1018 electrons/amp sec x 10-5 amp sec), which also happens to be approximately the maximum amount of excess charge that can be deposited on a one square meter surface before sparking becomes likely. When these electrons were transferred while the two surfaces were in contact, the electrons only moved a distance of about one atomic diameter, and the move didn’t produce any detectable signal to the outside world, except that the two sheets are now attracting each other. The number of electrons that transfer is typically only a tiny percentage of the available electrons on the surface. A charge of 10-5 amp sec per square meter only represents about one electron per 300,000 surface atoms (although each polymer “molecule” contains thousands of atoms).
“Static effects” only occur if charges become isolated (i.e., if the two surfaces are pulled apart). The two sheets begin together (frame 1 of Fig.1) and are in a “minimum energy state”; that is, they would like to stay the way they are. As long as they are in close contact, there is no high voltage generated and no chance of a spark. Because they are attracting each other, some work will be required in order to pull them apart. Ironically, that “work” is what will actually generate the high voltages and any associated sparks. (The situation is a lot like pulling an elastic band; it can become somewhat dangerous if stretched very far.) Fig. 1 shows the sheets at three separation distances: 0 cm, 1 cm, and 10 cm. All of the important static quantities are shown at each of the three separations. Formulas are available for all these parameters.
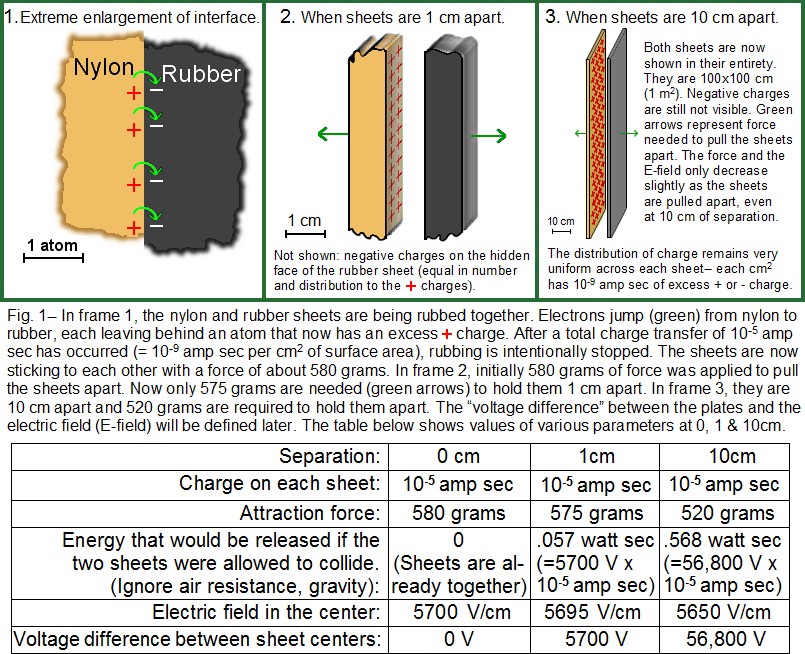
The electric field (E-field): Consider a single atom that is missing an electron (therefore it has one excess positive charge). Place this atom close to an object that is negatively charged (excess electrons). The (positive) atom will be attracted toward the (negative) object. We could add more charged objects to this environment. Any additional negative object will attract the atom, and any positive object will repel it. Each object pulls or pushes on the atom with a certain amount of force; the sum of all these forces is the “net force” acting on the atom. (These forces are vectors, so both the strength and direction of each force must be considered when adding the forces. The sum of all the forces is also a vector.) The electric field (E-field) is a vector that points in the same direction as the net force acting on a positively- charged atom. The strength of the E-field is proportional to the total force acting on the positive atom, as will be clarified.
The E-field can be defined more precisely as follows: Begin with a distribution of positive and negative charges as in Fig. 2. The E-field is defined at any given location as follows: place a small positive charge (at rest) at that location. This is the small red dot in Fig. 2. If the small charge doesn’t subsequently move, it means that all of the other charges produce forces that exactly cancel out, meaning that the E-field is zero at that location (an unlikely coincidence). If the small charge does begin to move, an E-field exists there. The direction of the E-field is the same direction that the small (positive) charge accelerates. The strength of the E-field is proportional to the net force acting on the small charge. In Fig. 2, the large red circle contains a lot of positive charge, so it repels the small positive charge with a force represented by the red arrow. The black circle contains some negative charge, which attracts (black arrow) the small positive charge. The E-field strength is measured in units of volts/cm(V/cm). If a positive charge of 1/100 amp sec were placed in an E-field of 1 V/cm, the force acting on the charge would be about 100 grams. (For comparison, 2 V/cm would exert 200 grams on a 1/100 amp sec charge.) As had been inferred previously from Fig. 1, 1/100 amp sec is quite a lot of positive charge, and any attempt to force this much charge into a volume of less that a few cubic meters would actually result in sparks, as the charges violently try to get away from each other. It is more common to encounter objects with charges of 10-6 amp sec or less. However, ambient E-field strength is commonly hundreds of V/cm, and is rarely as low as 1 V/cm.

Strength and nominal range of the E-field: The E-field from a charged object (such as the large red or black spheres in Fig. 2) becomes weaker at increasing distance, as you might expect. (The dependence is “one over the distance squared”.) However, the E-field from a charged wall (as in frame 3 of Fig. 1) does not decrease much with distance, at least if the E-field is being measured very close to the wall– less than about 1/3 of the wall width. (Note the small difference in E-field in Fig. 1 between frame 2 and frame 3. If a charged wall is 1 meter wide, the E-field does decrease rapidly with distance, but only if measured more than a few meters away. In contrast, the field is fairly constant within a few cm, at the center of the wall.) This wall effect is a consequence of adding up all the contributions of each charge on the wall, remembering that each is a vector. Every proton and electron in the universe theoretically contributes to the E-field at a given location; however, each neutral atom contributes zero to the field because the contribution of the electrons in the atom is of the same strength but of exactly opposite direction as that of the protons. Only those regions which have excess positive or negative charge will effectively contribute. Even this contribution falls off rapidly with distance. As a consequence, most static effects come from sources no more than a few meters away (exception: atmospheric electricity/lightning, which has a range of kilometers due to the enormous amounts of charge involved).
The state of “high voltage” occurs wherever a large number of excess + or – charges are forced into a relatively small volume. They try to repel each other, and if some of the charge manages to escape from the confining volume, that charge will quickly accelerate to high speed (and thus high kinetic energy) as it flees from the rest of the charge that remained behind. Remember that the E-field is related to the total electric force that acts upon a specific amount of charge. Similarly, voltage is related to the energy acquired by a specific amount of charge when it moves along its trajectory. The moving charge picks up this energy because it is moving through an E-field which is capable of accelerating it. Specifically, the voltage difference in moving from point “A” to point “B” is equal to the amount of energy that would be acquired by one amp sec of charge if it were moved from “A” to “B”. Energy is measured in watt sec (also called “joules”).
Voltage increases with increases as charged objects are separated. The movement of a charge under the influence of an E-field is similar to the movement of a mass in a gravitational field; the amount of energy picked up by a falling mass is proportional to the distance it has fallen. If a mass falls only a fraction of a cm, it will do much less damage than if it falls several meters. Similarly, in Fig. 1 frame 3, if some of the negative charge (electrons) escaped (via a spark) from the right sheet and flowed 10 cm through the air to the left sheet, the event would be associated with a certain amount of energy. That energy would create some light and sound and some local heating (although transient heat is hard to measure). This charge escape can be initiated by taking a small piece of metal foil that has sharp corners, and adhering it somewhere onto the charged side of the rubber sheet. If the same amount of charge had escaped instead when the sheets were 1 cm apart (frame 2), it would be associated with only about 1/10 the energy. In frame 1 of Fig. 1, there would be no energy released if a group of electrons “leaked” backward from the rubber to the nylon. If all the electrons on the right sheet escaped to the left sheet, the energy released would be as shown (in watt sec), for 0, 1 and 10 cm separations in the table of Fig.1. (Positive charges act as though they were “positive” electrons, but the physical mechanism of positive charge escape is hard to represent in a diagram, so I will only give examples of negative charge movements. However, it is equally possible to initiate a positive charge escape at the nylon sheet, which would have the same effect as an electron escape at the rubber.)
Voltage estimate if the sheets are separated very far: As was just said, one can obtain a high voltage (and its associated risks), by starting with surface charging as in Fig. 1 frame 1. However, there is no voltage difference between the sheets in frame 1, and thus no energy available to do damage. In frame 2, + and – charges are now separated and they can do some damage, but they can only travel 1 cm before they recombine, which is not associated with an extremely large amount of energy. Almost 10x the energy is available in frame 3. The highest voltage is obtained if the two sheets are separated by a distance that is large compared to their width. If the sheets of Fig. 1 were separated by 10 meters or more, the nylon would be at about +200,000 V (+200 kV) and the rubber would be about -200,000 V (both voltages are measured with respect to earth ground). The voltage difference between the sheets would be about 400,000 V. (These numbers also suppose that any grounded object is at least 10 meters from either sheet.) In this configuration, electrons on the rubber sheet are repelled by each other. If a fraction of them escape (such as by touching the rubber with a small sharp piece of non- grounded metal), they will be accelerated away from the rubber, pushed by the E-field from the electrons that remain on the rubber. This field is strong only within a few meters of the rubber. If the escaped electrons go on a path in which they eventually collide with a grounded conductor (earth), they will have gone through a voltage change of 200,000 V. If they were instead allowed to collide with the nylon, they would acquire twice as much energy and go through a voltage change of 400,000 V.
A formula to estimate voltage of compact objects: If an excess of +10-6 amp sec is forced into a sphere of diameter 100 cm, the voltage at the surface will be +18,000 volts (18 kV). Similarly, any object with 10-6 amp sec of charge and dimensions of about 100 cm will have a similar voltage. This assumes that the sphere is isolated from the Earth (ground) and from significantly charged objects; the number 18,000 V is only correct if the sphere is at least several hundred cm away from these. If the sphere is instead near the ground, any escaping charges will be attracted to the ground (to be explained later). Therefore, escaping charges will not travel very far before reaching “zero volts” of the Earth ground, and they do not pick up very much energy before they collide with the ground. This effect causes the voltage to be much less than 18,000 V if the sphere is brought close to the ground, even if it still has +10-6 amp sec of charge. (This is like a high diver having a lot of potential energy when up high but much less potential energy if the diving platform is lowered close to the ground.) The voltage on an isolated sphere (or any object) is directly proportional to the amount of excess charge on it. The voltage is inversely proportional to the diameter of the sphere, so a 50cm isolated sphere with +10-6 amp sec will be at +36,000 V. (Notice that the voltage is proportional to “one over the diameter”, not “one over the diameter squared”.) The explicit formula.
The distribution of charges is the only factor that creates electric field. As expected, the total electric field that a charged object (or a clump of charge) experiences is the directional (vector) sum of all the fields that all other charges produce at the location of the object. “Other charges” refers to all charges in the universe other than the charge in the object itself. (A charged object does not exert any overall force on itself.) In general, faraway charges produce relatively little force, because of the “one over distance squared” law. One feature that may not be expected is that metal does not in itself block electric field or force. In order to calculate total force, add the effect of all charges including charges on the surface (or inside) of any metal in the environment, and then ignore the presence of the metal. Metals and other conductors only alter the electric field because charges shift to a new distribution when exposed to an electric field inside the metal. In a metal or other conductor, electrons can move freely anywhere inside the metal (but they cannot jump off the surface of the metal into the air unless the conditions are right for a spark). You only need to know the location, polarity, and amount of the charges on (or in) the metal. Then calculate the forces from those charges as though they were hanging in space and the metal was not there. Insulators can also contain a distribution of charges, and once again, pay attention to the charges but ignore the presence of the insulator. (You may have heard of the “dielectric effect”, which is caused by the very limited movement of charges in an insulator. Charges in an insulator are like dogs on leashes; each can only move a short distance from their parent atom. They move a little in response to an electric field, and this new distribution of charges does affect the exterior electric field, but only the location, polarity, and amount of the charges, once they have moved to their final locations, will alter the electric field outside the insulator.)
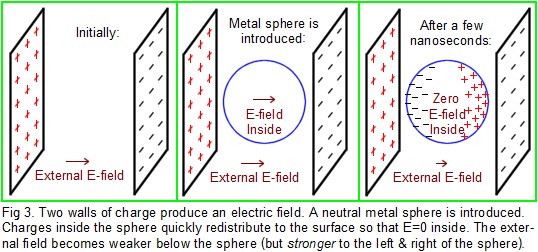
Mobile vs. Stationary Charges: In Fig.3, there are two charged walls. Electrons have been removed from the left wall and deposited on the right wall. Therefore, there is an electric field pointing rightward. If a single proton is released in the middle, it will accelerate toward the right, whereas an electron will accelerate left. Suppose a metal sphere is suddenly introduced between the walls. Remember that a fraction of the electrons in the metal are free to move around inside the metal, although they cannot go any farther than the surface of the sphere (unless the voltage is high enough for a spark; then electrons can either jump off the sphere into air, or they could jump from air to the sphere). If the E-field is relatively weak so that there is no sparking, then the freely-moving electrons inside the sphere will accelerate to the left until they arrive at the surface, where they can go no farther. On the right side of the sphere, a slight shortage of electrons will appear. This shift in the distribution of electrons in the metal occurs simply because the free electrons are each responding to the E-field that is coming from the walls. Electrons in the metal sphere will continue moving in this fashion for a brief time. Note that electrons accumulate on the left side of the sphere (producing a negative shell of charge on the left) and electrons leave the right side of the sphere (producing a positive shell on the right); this distribution of electrons on the surface of the sphere will alter the E-field in the center of the sphere. In fact, the charges on the sphere will produce a field in the opposite direction of the field from the walls. The net effect is that the electron redistribution decreases the E-field inside the metal. Electrons in the metal will continue to move in this fashion (as the internal field becomes weaker and weaker) until a stable condition is reached. That stable condition occurs when electrons are no longer moving around in the metal. In order not to need to move, the E-field must be zero everywhere inside the metal, and electrons will end up the proper distribution to make the field zero, but only inside the metal. (Imagine that a region of the metal had a nonzero field. Then any free electrons in that region would begin to move in response to the field, and they would move in a direction that reduced the total field. Soon the field would become zero in that region, and then electrons stop moving.) Typically only a few nanoseconds are required for this stable distribution to take effect in metal, but it is much slower in poor conductors like glass, where it may take seconds. In metals, all the zones of excess negative or positive charge end up within one atomic diameter of the surface (the inside of the surface, of course).
An insulator is a ver “slow” yet regardless of conduction, charge is always conserved. Charges in a conductor are mobile, and can move throughout the conductor. Their net effect is to reduce the value of E to zero everywhere inside the conductor, but only if the charges can move fast enough to keep up with the speed at which any external electric field is changing. Charges inside an insulator can rapidly only move a small distance, and are pinned to their parent atoms. Essentially they cannot move, but only if the insulator is perfect. Real insulators are imperfect and charge can slowly leak the entire length of the insulator such that the E-field inside an imperfect insulator slowly reduces toward zero. Most plastics are fairly good insulators. Glass can be considered a good insulator over time scales that are shorter than a second. Over a time scale of minutes or longer, glass is essentially a conductor. At moderate humidity, concrete, drywall, wood, and paper/cardboard all have conductive properties similar to glass. A perfect insulator has the property that if charges are deposited on it (or inside it), the charges simply stay in the same locations they were originally placed. For example, assume there is no external electric field around a vinyl sphere. If electrons are sprayed onto one hemisphere, they will stay on that hemisphere for hours. The asymmetric distribution of electrons will create an E-field inside the sphere, but the charges in the sphere are not mobile, so they cannot respond much to the field. If the sphere were metal, the E-field would be neutralized in nanoseconds because the excess electrons would spread out uniformly over the surface of the whole sphere. (This response would reduce the field to zero everywhere inside the metal sphere. Note that the total number of excess electrons does not change; charge is “conserved” unless it was given a path by which it could leave the sphere. Therefore the metal sphere, like the vinyl one, would still carry excess negative charge. The excess charge on the metal just rapidly becomes uniformly spread out over the surface.)
Air itself can slowly neutralize static charges charges. There is one more significant “conductor” to consider. It is air. Under normal conditions, air is a conductor, but only over the time scale of hours. A very small percentage of air is made up of ions; these are collections of typically 10 to 25 atoms held together either by an excess electron (- ion) or by the lack of one electron (+ ion). Both + and – ions can coexist for minutes without neutralizing each other. They are constantly being formed, although at room temperature, an energy source is needed to form them. This source is typically radioactive decay (especially from radon and cosmic rays), evaporation of water, and heat or combustion above about 1000 degrees F. If a perfectly-insulating sphere with excess electrons is left in the air for a long time, it will become completely discharged. It will eventually lose all excess charge and become neutral (as long as there is no other source of charge). This discharge happens when the + air ions are attracted to the – charged surface. Each ion collides with the surface. In this case (a negative surface), each + ion steals one electron from the vinyl surface. Then the ion becomes neutral and it can no longer hold itself together (+ ions usually contain water molecules, nitrogen atoms, and typically a hydrogen atom), so the component atoms/molecules then fly away (each now neutral). An ionizer enriches the air with many more ions (usually measured in ions per cubic centimeter) than are normally present. Most ionizers that are used for static control produce roughly equal numbers of + and – ions. (If an ionizer produced more of one polarity than the other, it would cause nearby surfaces to become charged with that polarity, which is undesirable for static prevention.) See additional information: About Air Ions.
Charge induction: As has been discussed, any process that charges two surfaces (while they were initially in proximity) can initiate static problems. However there is another charging process called charge induction that is not as intuitive. In Fig.4, there is a metal slab (blue) that is being exposed to an E-field and is in a stable state of internal charge distribution, similar to the picture on the right side of Fig.3. However, Fig.4 has only one charged wall (black). As with Fig.3, this charged wall creates an E-field that causes the distribution of charges in the metal. This distribution, as shown, is the only distribution that makes the E-field zero inside the sphere while conserving charge. The black wall, with 8 negative charge “units” (8 “-” signs), will produce a certain strength of E-field. The blue slab, with 4 units of + charge on its right and 4 -units on its left, will internally produce the same strength of E-field, but in the opposite direction. Therefore the field is zero inside the slab, and the total charge in the slab remains zero (+4 – 4 = 0) for charge conservation. The electrons at the left side of the slab experience an E-field and are pushed toward the left but cannot escape.
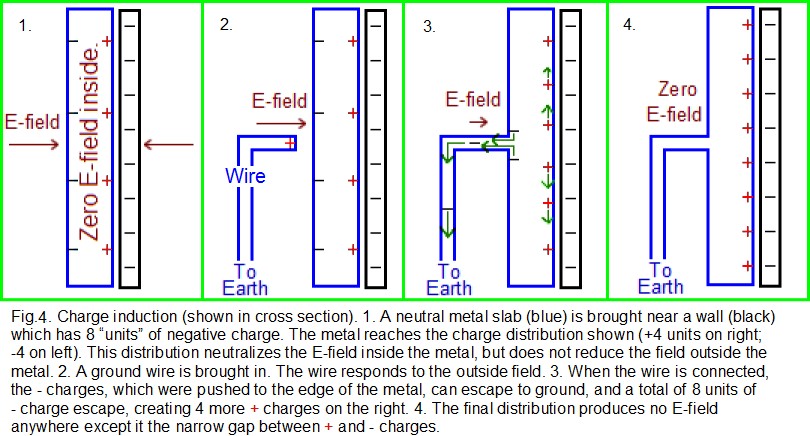
A wire is now brought in as shown in the second cell of Fig.4, also in blue. One side of the wire is “grounded”; that is, it touches the Earth (such as at humid soil, which is conductive). Note that the Earth itself is much like a huge metal sphere which is in the simplest possible state: there is no overall excess of + or – charge on the Earth, and there is no external E-field. (Atmospheric electricity does cause some localized surface charging, but the effect is not important in explaining how grounding works.) Therefore, the Earth has essentially zero charge on its surface. Soon after the wire touches the metal slab, charges must move to a distribution such that the E-field is zero everywhere in the metal slab and in the wire. Before the electrons had a chance to move down the wire, there was a strong E-field both inside the wire and acting upon the electrons near the wire. The field then forced the electrons to move down the wire to ground. More than just the 4 “units” of electrons (shown as 4 negative signs) moved down the wire. Once the 4 units had gone, there were still only 4 “+units” on the right side of the slab, but 8 “-units” of charge on the left side of the wall. This imbalance causes another 4 “- units” of electrons to flee down the wire, creating 4 new “+ units” of charge on the right, as shown on the right side of Fig. 4.
Suppose now that wire in Fig. 4 is removed, and then the charged wall is pulled away. That will leave the metal slab with excess + charges, and therefore at an elevated voltage. The four-step process of bringing a charged object near a conductor (but not touching the conductor), then touching the opposite side of the conductor with a ground, then removing the ground, then removing the charged object– is called charge induction onto the conductor. The conductor will become the opposite polarity of the charged object.
Most static charging is caused either by surface charge transfer (which usually charges insulators but not conductors) and charge induction (which only charges conductors). Surface charging can also happen on either conductors or insulators if ions are shot onto the surface or if the surface is exposed to a high voltage DC power supply (which will cause ions to adhere to the surface).

